数据结构-借假修真

数据结构

• 数组、字符串
• 链表
• 栈
• 队列
• 双端队列
• 树

数组、字符串（Array & String）

字符串转化

翻转字符串“algorithm”。
用两个指针，一个指向字符串的第一个字符 a，一个指向它的最后一个字符 m，然后互相交换。交换之后，两个指针向中央一步步地靠拢并相互交换字符，直到两个指针相遇。这是一种比较快速和直观的方法

• 数组的优缺点
  • 构建非常简单
  • 能在O(1)的时间里根据数据的下标查询某个元素

• 数组的缺点

  • 构建时必须分配一段连续的空间

  • 查询某个元素是否存在时需要遍历整个数组，耗费 O(n) 的时间（其中，n 是元素的个数）

  • 删除和添加某个元素时，同样需要耗费 O(n) 的时间

    链表 LinkedList

    单链表：链表中的每个元素实际上是一个单独的对象，而所有对象都通过每个元素中的引用字段链接在一起。

双链表：与单链表不同的是，双链表的每个结点中都含有两个引用字段。

• 优缺点
  • 能在 O(1) 时间内删除或者添加元素，前提是该元素的前一个元素已知，当然也取决于是单链表还是双链表，在双链表中，如果已知该元素的后一个元素，同样可以在 O(1) 时间内删除或者添加该元素
  • 缺点：
    • 不像数组能通过下标迅速读取元素，每次都要从链表头开始一个一个读取；
    • 查询第 k 个元素需要 O(k) 时间
• 场景：如果要解决的问题里面需要很多快速查询，链表可能并不适合；如果遇到的问题中，数据的元素个数不确定，而且需要经常进行数据的添加和删除，那么链表会比较合适。而如果数据元素大小确定，删除插入的操作并不多，那么数组可能更适合

栈 Stack

特点：栈的最大特点就是后进先出（LIFO）对于栈中的数据来说，所有操作都是在栈的顶部完成的，只可以查看栈顶部的元素，只能够向栈的顶部压⼊数据，也只能从栈的顶部弹出数据。

实现：利用一个单链表来实现栈的数据结构。而且，因为我们都只针对栈顶元素进行操作，所以借用单链表的头就能让所有栈的操作在 O(1) 的时间内完成。

应用场景：在解决某个问题的时候，只要求关心最近一次的操作，并且在操作完成了之后，需要向前查找到更前一次的操作。

如果打算用一个数组外加一个指针来实现相似的效果，那么，一旦数组的长度发生了改变，哪怕只是在最后添加一个新的元素，时间复杂度都不再是 O(1)，而且，空间复杂度也得不到优化。

队列 Queue

特点：和栈不同，队列的最大特点是先进先出（FIFO），就好像按顺序排队一样。对于队列的数据来说，我们只允许在队尾查看和添加数据，在队头查看和删除数据。

实现：可以借助双链表来实现队列。双链表的头指针允许在队头查看和删除数据，而双链表的尾指针允许我们在队尾查看和添加数据。

应用场景：直观来看，当我们需要按照一定的顺序来处理数据，而该数据的数据量在不断地变化的时候，则需要队列来帮助解题。在算法面试题当中，广度优先搜索（Breadth-First Search）是运用队列最多的地方。

双端队列 Deque

特点：双端队列和普通队列最大的不同在于，它允许我们在队列的头尾两端都能在 O(1) 的时间内进行数据的查看、添加和删除。

实现：与队列相似，我们可以利用一个双链表实现双端队列。

应用场景：双端队列最常用的地方就是实现一个长度动态变化的窗口或者连续区间，而动态窗口这种数据结构在很多题目里都有运用

树

普通二叉树、平衡二叉树、完全二叉树、二叉搜索树、四叉树（Quadtree）、多叉树（N-ary Tree）

• 树的遍历
  • 前序遍历（Preorder Traversal）
    • 先访问根节点，然后访问左子树，最后访问右子树。在访问左、右子树的时候，同样，先访问子树的根节点，再访问子树根节点的左子树和右子树，这是一个不断递归的过程
  • 中序遍历 （Inorder Traversal）
    • 先访问左子树，然后访问根节点，最后访问右子树，在访问左、右子树的时候，同样，先访问子树的左边，再访问子树的根节点，最后再访问子树的右边。
  • 后序遍历 （Postorder Traversal）
    • 先访问左子树，然后访问右子树，最后访问根节点。
• 二叉搜索树：
  • 对于每个节点来说，该节点的值比左孩子大，比右孩子小，而且一般来说，二叉搜索树里不出现重复的值。

高级数据结构

• 优先队列

• 图

• 前缀树

• 线段树

• 树状数组

优先队列 （Priority Queue）

• 特点
  能保证每次取出的元素都是队列中优先级别最高的。优先级别可以是自定义的，例如，数据的数值越大，优先级越高；或者数据的数值越小，优先级越高。优先级别甚至可以通过各种复杂的计算得到
• 应用场景
  从一堆杂乱无章的数据当中按照一定的顺序（或者优先级）逐步地筛选出部分乃至全部的数据。

• 实现

  • 本质是一个二叉对结构 Binary Heap，利用数组结构来实现的完全二叉树
  • 换句话说，优先队列的本质是一个数组，数组里的每个元素既有可能是其他元素的父节点，也有可能是其他元素的子节点，而且，每个父节点只能有两个子节点，很像一棵二叉树的结构

  • 特性：

    • 1. 数组里的第一个元素 array[0] 拥有最高的优先级别。
    • 2. 给定一个下标 i，那么对于元素 array[i] 而言：

      它的父节点所对应的元素下标是 (i-1)/2

      它的左孩子所对应的元素下标是 2×i + 1

      它的右孩子所对应的元素下标是 2×i + 2

    • 3. 数组里每个元素的优先级别都要高于它两个孩子的优先级别。

  • 操作

    • 向上筛选 sift up/bubble up
      • 当有新的数据加入到优先队列中，新的数据首先被放置在二叉堆的底部
      • 不断进行向上筛选的操作，即如果发现该数据的优先级别比父节点的优先级别还要高，那么就和父节点的元素相互交换，再接着往上进行比较，直到无法再继续交换为止。
        时间复杂度：
        由于二叉堆是一棵完全二叉树，并假设堆的大小为 k，因此整个过程其实就是沿着树的高度往上爬，所以只需要 O(logk) 的时间。

    • 向下筛选 （sift down /bubble down）

      • 当堆顶的元素被取出时，要更新堆顶的元素来作为下一次按照优先级顺序被取出的对象，需要将堆底部的元素放置到堆顶，然后不断地对它执行向下筛选的操作。

      • 将该元素和它的两个孩子节点对比优先级，如果优先级最高的是其中一个孩子，就将该元素和那个孩子进行交换，然后反复进行下去，直到无法继续交换为止
        时间复杂度：整个过程就是沿着树的高度往下爬，所以时间复杂度也是 O(logk)。

      因此，无论是添加新的数据还是取出堆顶的元素，都需要 O(logk) 的时间。

初始化

优先队列的初始化是一个最重要的时间复杂度，是分析运用优先队列性能时必不可少的，也是经常容易弄错的地方
举例：有 n 个数据，需要创建一个大小为 n 的堆。

误区：每当把一个数据加入到堆里，都要对其执行向上筛选的操作，这样一来就是 O(nlogn)。

解法：在创建这个堆的过程中，二叉树的大小是从 1 逐渐增长到 n 的，所以整个算法的复杂度经过推导，最终的结果是 O(n)。

图（Graph）

基本知识点

图可以说是所有数据结构里面知识点最丰富的一个，最基本的知识点如下

• 阶（Order）、度：出度（Out-Degree）,入度（In-Degree）
• 树（Tree）、森林(Forest)、环（Loop）
• 有向图（Directed Graph）,无向图(Undirected Graph)、完全有向图、完全无向图
• 连通图（Connected Graph）、连通分量（Connected Component）
• 存储和表达方式：邻接矩阵（Adjacency Matrix）、邻接链表（Adjacency List）

围绕图的算法

• 图的遍历：深度优先、广度优先
• 环的检测：有向图、无向图
• 拓扑排序
• 最短路径算法：Dijkstra（狄更斯特拉）、Bellman-Ford、Floyd Warshall
• 连通性相关算法：Kosaraju、Tarjan、求解孤岛的数量、判断是否为树
• 图的着色、旅行商问题等

必知必会：

• 图的存储和表达方式：邻接矩阵（Adjacency Matrix）、邻接链表（Adjacency List）

• 图的遍历：深度优先、广度优先

• 二部图的检测（Bipartite）、树的检测、环的检测：有向图、无向图

• 拓扑排序

• 联合-查找算法（Union-Find）

• 最短路径：Dijkstra、Bellman-Ford

其中，环的检测、二部图的检测、树的检测以及拓扑排序都是基于图的遍历，尤其是深度优先方式的遍历。而遍历可以在邻接矩阵或者邻接链表上进行，所以掌握好图的遍历是重中之重！因为它是所有其他图论算法的基础。

前缀树(Trie)

应用场景
前缀树被广泛地运用在字典查找当中，也被称为字典树。
经典应用:

• 网站上的搜索框会罗列出以搜索文字作为开头的相关搜索信息，这里运用了前缀树进行后端的快速检索。

• 汉字拼音输入法的联想输出功能也运用了前缀树。
  性质：

  • 1. 每个节点至少包含两个基本属性。

children：数组或者集合，罗列出每个分支当中包含的所有字符

isEnd：布尔值，表示该节点是否为某字符串的结尾

• 2. 前缀树的根节点是空的

所谓空，即只利用到这个节点的 children 属性，即只关心在这个字典里，有哪些打头的字符。

• 3. 除了根节点，其他所有节点都有可能是单词的结尾，叶子节点一定都是单词的结尾。

实现

• 基本操作：创建、搜索

  • 创建

    • 遍历一遍输入的字符串，对每个字符串的字符进行遍历

    • 从前缀树的根节点开始，将每个字符加入到节点的 children 字符集当中。

    • 如果字符集已经包含了这个字符，则跳过。

    • 如果当前字符是字符串的最后一个，则把当前节点的 isEnd 标记为真。

  前缀树真正强大的地方在于，每个节点还能用来保存额外的信息，比如可以用来记录拥有相同前缀的所有字符串。因此，当用户输入某个前缀时，就能在 O(1) 的时间内给出对应的推荐字符串。

  • 搜索
    • 与创建方法类似，从前缀树的根节点出发，逐个匹配输入的前缀字符，如果遇到了就继续往下一层搜索，如果没遇到，就立即返回。
      

      线段树 （Segment Tree）

• 就是一种按照二叉树的形式存储数据的结构，每个节点保存的都是数组里某一段的总和。
• 适用于数据很多，而且需要频繁更新并求和的操作。
• 时间复杂度O(logn)

实现

数组是 [1, 3, 5, 7, 9, 11]，那么它的线段树如下。

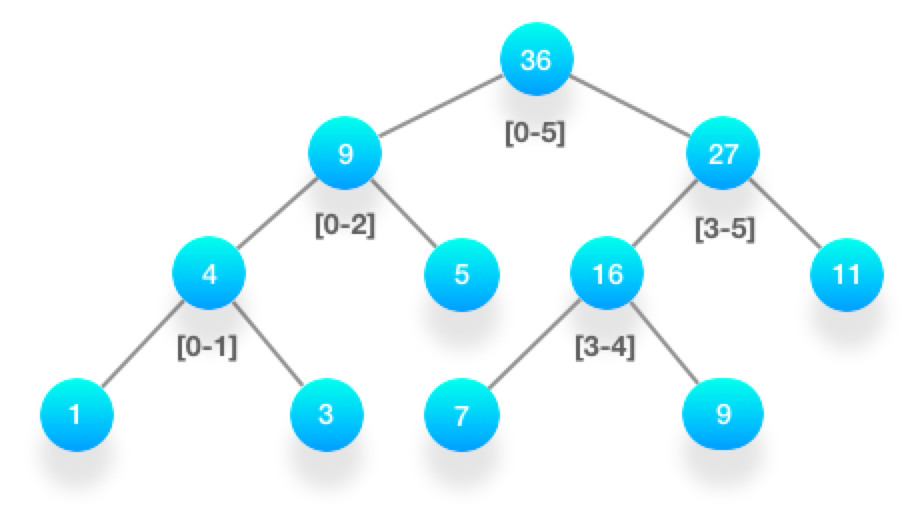
根节点保存的是从下标 0 到下标 5 的所有元素的总和，即 36。左右两个子节点分别保存左右两半元素的总和。按照这样的逻辑不断地切分下去，最终的叶子节点保存的就是每个元素的数值

解法：

1. 更新数组里某个元素的数值

从线段树的根节点出发，更新节点的数值，它保存的是数组元素的总和。修改的元素有可能会落在线段树里一些区间里，至少叶子节点是肯定需要更新的，所以，要做的是从根节点往下，判断元素的下标是否在左边还是右边，然后更新分支里的节点大小。因此，复杂度就是遍历树的高度，即 O(logn)。

 

2. 对数组某个区间段里的元素进行求和

方法和更新操作类似，首先从根节点出发，判断所求的区间是否落在节点所代表的区间中。如果所要求的区间完全包含了节点所代表的区间，那么就得加上该节点的数值，意味着该节点所记录的区间总和只是所要求解总和的一部分。接下来，不断地往下寻找其他的子区间，最终得出所要求的总和

树状数组（Fenwick Tree /Binary Indexed Tree）

特点
树状数组的数据结构有以下几个重要的基本特征。

它是利用数组来表示多叉树的结构，在这一点上和优先队列有些类似，只不过，优先队列是用数组来表示完全二叉树，而树状数组是多叉树。

树状数组的第一个元素是空节点。

如果节点 tree[y] 是 tree[x] 的父节点，那么需要满足条件：y = x - (x & (-x))。